Identification of human control during walking

Jason K. Moore j.k.moore19@csuohio.edu

Human Motion and Control Laboratory [hmc.csuohio.edu]

Cleveland State University, Cleveland, Ohio, USA

June 6, 2014

Background

Doctoral work on identification of the human controller in the bicycle balancing task.

TU Delft 2008-2009

UC Davis 2009-2012

Lower Extremity Exoskeletons

Clips collected from [1], [2], [3], and [4].

Prior Art

• Identification during standing: quite a lot
• Identification during gait [Rouse, ...]
• Piecewise nonlinear impedance control: [Goldfarb, ...]
• Identification of active and passive dynamics in limb movement [Kearney, ...]
• Step variation quantifications under perturbations: [Collins, Hof, ..]
• Impedance control and ID

Rouse 2011-2014

Elliot Rouse and co-authors identified the "controller" for the ankle from external perturbations.

• Ankle model identification in stance phase
• Ramp perturbations from a rotating force platform
• ~400 steps per subject
• Identified canonical model: \(T = I (\ddot{\theta}) + C (\dot{\theta}) + K \dot(\theta) \)

Neuromuscular System

Idealized Gait Feedback Control

Typical Dynamic Gait Lab Measurements

• Ground reaction loads at each foot
• Inertial musculoskeletal marker positions
• Body segment angular velocity
• Point accelerations
• Muscle activation: EMG
• Travel (or belt) speed

Computed Estimates

• Joint torques
• Joint angles, angular velocities, angular accelerations
• Muscle forces and lengths
• Center of pressure

What sensors are likely most important for human gait control?

• Proprioception (muscle spindles, Golgi tendon): relative position of body parts, muscle tension (gait timing)
• Vestibular (semicircular canals, otoliths): angular rotation and rate, linear acceleration (horizontal and vertical), gravity direction
• Sight: global and body relative orientation, position
• Touch: force on feet

Sensors available to external prosthetics

• Relative joint position
• Body fixed angular velocity
• Body fixed point accelerations
• Force transducers and pressure sensors

Closed Loop System Identification

Closed loop system id is possible, but one must be aware of several issues. Here are two common methods:

• Direct Approach: measure \(u\), \(y\) where \(P\) and \(C\) are unknown
• Indirect Approach: measure \(r\), \(y\) where either \(P\) or \(C\) is known

Direct Approach

Measure \(u(t)\) and \(y(t)\), ignore feedback, and fit a model to the data.

If the direct method is used in the frequency domain the external perturbations must be high enough to bias the identification towards the controller, rather than the plant. (Kearny 1990, Ljung 1999, van der Kooij 2005)

\[ G(s) = \frac{y(s)}{u(s)} = \frac{P(s) \Phi_r(\omega) - C(s) \Phi_v(\omega)} {\Phi_r(\omega) + |C(s)|^2 \Phi_v(\omega)} \]

If \( \Phi_r(w) >> \Phi_v(\omega) \) : \( G(s) = P(s) \)

If \( \Phi_v(w) >> \Phi_r(\omega) \) : \( G(s) = -\frac{1}{C(s)} \)

Direct Approach

But time domain identification may be possible if the bias is reduced by one or all of the following:

• The closed loop data is informative
• \(r\) is persistently excited
• Nonlinear or time varying or complex (high order) regulators
• Using suitable pre-filtering, i.e. inclusion of a good noise model
• Reducing the feedback contribution to the input spectrum \(\Phi u\)
• Large signal to noise ratio

Controller Equations

\[ \mathbf{m}(t) = \mathbf{m}_0(\varphi) + \mathbf{K}(\varphi) [\mathbf{s}_0(\varphi) - \mathbf{s}(t)] \\ \] \[ \mathbf{m}(t) = \mathbf{m}^*(\varphi) - \mathbf{K}(\varphi) \mathbf{s}(t) \] where \[ \mathbf{m}^*(t) = \mathbf{m}_0(\varphi) + \mathbf{K}(\varphi) \mathbf{s}_0(\varphi) \]

Gain Matrix

Sensors

Assume that a lower limb exoskeleton can sense relative orientation and rate of the right and left planar ankle, knee, and hip angles.

\(\mathbf{s}(t) = \begin{bmatrix} s_1 & \dot{s}_1 & \ldots & s_q & \dot{s}_q \end{bmatrix} \) where \(q=6\)

Controls (plant inputs)

Assume that the exoskeleton can generate planar ankle, knee, and hip joint torques.

\(\mathbf{m}(t) = \begin{bmatrix}m_1 & \ldots & m_q \end{bmatrix} \) where \(q=6\)

Gain Matrix [Proportional-Derivative Control]

\( \mathbf{K}(\varphi) = \begin{bmatrix} k(\varphi)_{s_1} & k(\varphi)_{\dot{s_1}} & 0 & 0 & 0 & \ldots & 0\\ 0 & 0 & k(\varphi)_{s_2} & k(\varphi)_{\dot{s_2}} & 0 & \ldots & \vdots\\ 0 & 0 & 0 & 0 & \ddots & 0 & 0\\ 0 & 0 & 0 & \ldots & 0 & k(\varphi)_{s_q} & k(\varphi)_{\dot{s}_q} \\ \end{bmatrix} \)

Linear Least Squares

With \(n\) time samples in each gait cycle and \(m\) cycles there are \(mnq\) equations and which can be used to solve for the \(nq(p+1)\) unknowns: \(\mathbf{m}^*(\varphi)\) and \(\mathbf{K}(\varphi)\). This is a classic overdetermined system of linear equations that can be solved with linear least squares.

\[\mathbf{A}\mathbf{x}=\mathbf{b}\] \[\hat{\mathbf{x}}=(\mathbf{A}^T\mathbf{A})^{-1}\mathbf{A}^T\mathbf{b}\]

• \(n=20,m\sim=400,q=6,p=12\)
• \(\mathbf{A}\) (48000 x 1560): joint angles and rates
• \(\mathbf{b}\) (48000 x 1): joint torques
• \(\mathbf{x}\) (1560 x 1): \(\mathbf{K}(\varphi)\) and \(\mathbf{m}^*(\varphi)\)

Experimental Protocol

• Full body 3D motion capture: 47 markers [1]
• Dual 6 DoF force plates on an actuated treadmill
• 2 minutes of unperturbed walking
• 8 minutes (~500 gait cycles) walking under longitudinal perturbations
• Three walking speeds: 0.8, 1.2, 1.6 m/s
• 11 subjects (male: 7, female: 4)
• Pseudo-random longitudinal perturbations: \(\pm 15\%\) nominal belt speed

Random Belt Speed Variations

Random Belt Speed Variations

Data Processing

1. Fill missing markers
2. Filter marker positions and ground reaction loads 6 hz low pass filter
3. Compute joint angles, rates, and torques using 2D inverse dynamics
4. Section data into variable duration gait cycles based on right foot heel strikes
5. Re-sample each gait cycle at 20 equally spaced samples
6. Construct the design matrix (regressor), \(\mathbf{A}\) and the output vector, \(\mathbf{b}\)
7. Solve for \(\mathbf{m}^*(\varphi)\) and \(\mathbf{K}(\varphi)\)
8. Compute regression statistics and visualize

Measurement Variations

Unperturbed

Perturbed

Gains: v=0.8 m/s

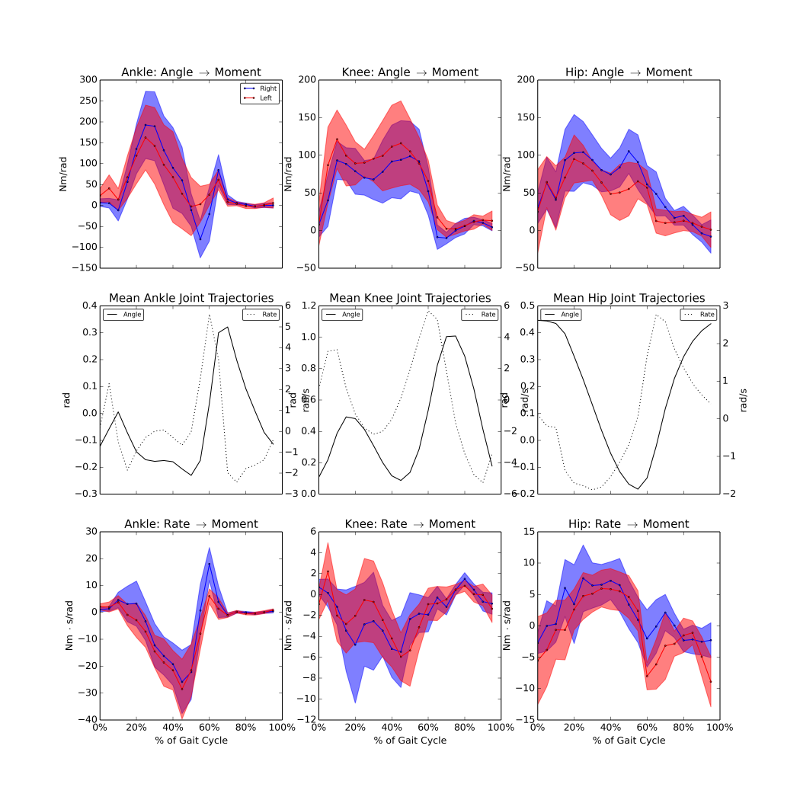
Gains: v=1.2 m/s

Gains: v=1.6 m/s

Gain variation with speed

How good is the model?

Model Fit Improvements With Control

• Identify \(\mathbf{m}^*\): \(nq\) parameters, mean VAF ~70%
• Identify \(\mathbf{m}^*\) and joint isolated \(\mathbf{K}\): \(3nq\) parameters, mean VAF ~75%
• Identify \(\mathbf{m}^*\) and \(\mathbf{K}\): \(nq(p+1)\) parameters, mean VAF ~80%

Summary

• External perturbations must be higher that sensor noise to have any hope of estimating control in this fashion.
• Similar gain patterns in each leg.
• Similar gain patterns and magnitudes in different subjects.
• The gains are low magnitude in the swing phase and higher in magnitude in the stance phase.
• Negative velocity gains do not make much sense yet. More investigation is needed.
• The model can predict the joint torques for independent data.
• Can we put this controller into an exoskeleton?

Future

• Different Controller Structures
• Additional sensors: acceleration, foot pressure, etc
• Add in neural time delays
• Remove clock from controller (state dependent)
• Non-linear control models: e.g. neural network.
• Use indirect system identification approach with plant model.
• Simulate plant with open loop controls plus identified feedback.
• Try out the controller on the Indego exoskeleton.

Indirect Identification: Shooting

Closed Loop Simulation + Genetic Algorithms, requires musculoskeletal model

• Closed Loop EoM: \( \dot{x} = f(x, u, t, k) \)
• Simulation Outputs: \( y = g(x, u, t) \)
• Measured marker positions, ground reaction loads, etc: \(y^m\)
• Cost function: \( J = \frac{1}{w_1}\sum_{i=0}^n || y_i - y_i^m || + \frac{1}{w_2} \int_0^T T^2 dt + \frac{1}{\mathrm{stability}} + \ldots\)
• Free parameters: \(k_j \ldots k_m\)

Advantages

• Results in a stable model with working controller
• Few optimization parameters
• Optimization can be parallelized

Disadvantages

• Computational load is really high: real time simulation for 8 min 100 hz may take 400 hrs with 3000 optimization iterations[1]
• Genetic algorithms may only get close to the global minimum
• Controller depends on plant fidelity

Indirect Identification: Direct Collocation

Constrained optimization of discretized model + gradient based large scale optimizer

• Cost Function: \[ J = \sum_{i=0}^n || y_i - y_i^m || \]
• Constraints: \[ 0 = f(\dot{x}, x, u, t, k) \]
• Optimizers: Sequential Quadratic Programming, Interior Point Optimization, etc
• Free parameters: \(x_1 \ldots x_n \), \(k_1 \ldots k_m\)

Advantages

• No simulation required: lower computational cost, 10 of hours instead of hundreds of hours [1]
• May get to the global optimum

Disadvantages

• Large number of unknowns \(n \times p + m\)
• Gradients of cost function and constraints required
• Stable simulation may not be guaranteed

Information

Contact

• HMC Lab: hmc.csuohio.edu
• My website: moorepants.info
• Email: j.k.moore@csuohio.edu

Slides

• moorepants.info/presentations

Source code for this analysis

• github.com/moorepants/walking-sys-id
• github.com/csu-hmc/Gait-Analysis-Toolkit

Data

• On its way!

Collaborators

• Antonie J. van den Bogert
• Sandra K. Hnat