Idealized Gait Feedback Control

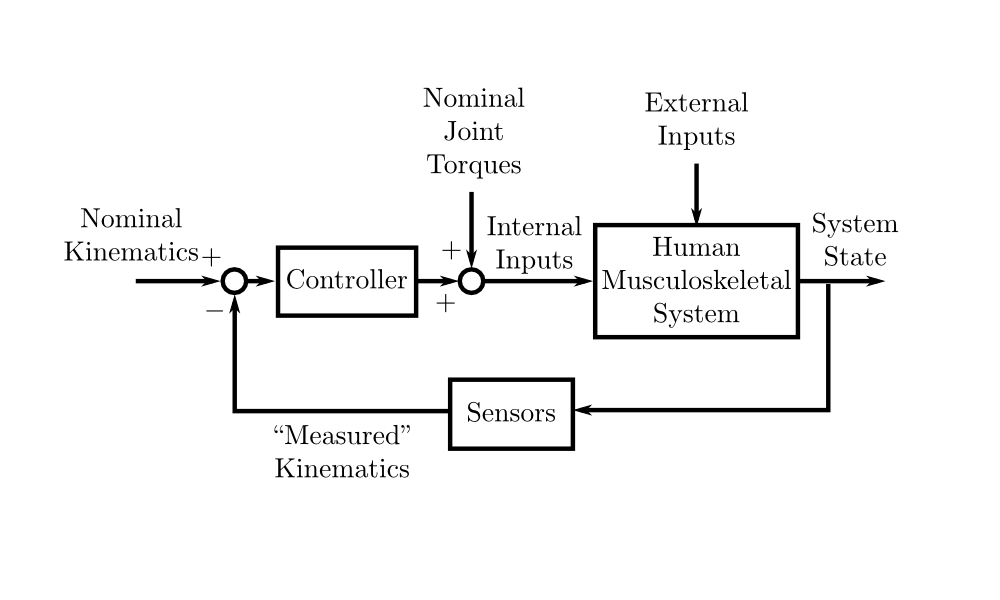
Idealized Gait Feedback Control

Controller Equations

$$\mathbf{m}(t) = \mathbf{m}_0(\varphi) + \mathbf{K}(\varphi) [\mathbf{s}_0(\varphi) - \mathbf{s}(t)] \\ $$ $$\mathbf{m}(t) = \mathbf{m}_0(\varphi) + \mathbf{K}(\varphi) \mathbf{s}_0(\varphi) - \mathbf{K}(\varphi) \mathbf{s}(t) \\ $$

Linear Form

$$\mathbf{m}(t) = \mathbf{m}^*(\varphi) - \mathbf{K}(\varphi) \mathbf{s}(t)$$

Map Human Control to Exoskeleton

Sensors

Assume that a lower limb exoskeleton can sense relative orientation and rate of the right and left planar ankle, knee, and hip angles.

$\mathbf{s}(t) = \begin{bmatrix} s_1 & \dot{s}_1 & \ldots & s_q & \dot{s}_q \end{bmatrix}$ where $q=6$

Controls (plant inputs)

Assume that the exoskeleton can generate planar ankle, knee, and hip joint torques.

$\mathbf{m}(t) = \begin{bmatrix}m_1 & \ldots & m_q \end{bmatrix}$ where $q=6$

Gain Matrix [Proportional-Derivative Control]

$\mathbf{K}(\varphi) = \begin{bmatrix} k(\varphi)_{s_1} & k(\varphi)_{\dot{s_1}} & 0 & 0 & 0 & \ldots & 0\\ 0 & 0 & k(\varphi)_{s_2} & k(\varphi)_{\dot{s_2}} & 0 & \ldots & \vdots\\ 0 & 0 & 0 & 0 & \ddots & 0 & 0\\ 0 & 0 & 0 & \ldots & 0 & k(\varphi)_{s_q} & k(\varphi)_{\dot{s}_q} \\ \end{bmatrix}$

Linear Least Squares

With $n$ time samples in each gait cycle and $m$ steps there are $mnq$ equations and which can be used to solve for the $nq(2q+1)$ unknowns: $\mathbf{m}^*(\varphi)$ and $\mathbf{K}(\varphi)$. This is a classic overdetermined system of linear equations that can be solved with linear least squares.

$$\mathbf{A}\mathbf{x}=\mathbf{b}$$

• $\mathbf{A}$: joint angles and rates
• $\mathbf{b}$: joint torques
• $\mathbf{x}$: $\mathbf{K}$ and $\mathbf{m}^*$

$$\mathbf{x}=(\mathbf{A}^T\mathbf{A})^{-1}\mathbf{A}^T\mathbf{b}$$

Experimental Protocol

• Full body motion capture: 47 markers
• Dual 6 DoF ground reaction forces
• 8 minutes (500+ steps) of longtidunal perturbations
• Three walking speeds: 0.8, 1.2, 1.6 m/s
• 10+ subjects
• Longitudinal perturbations

Random Belt Speed Variations

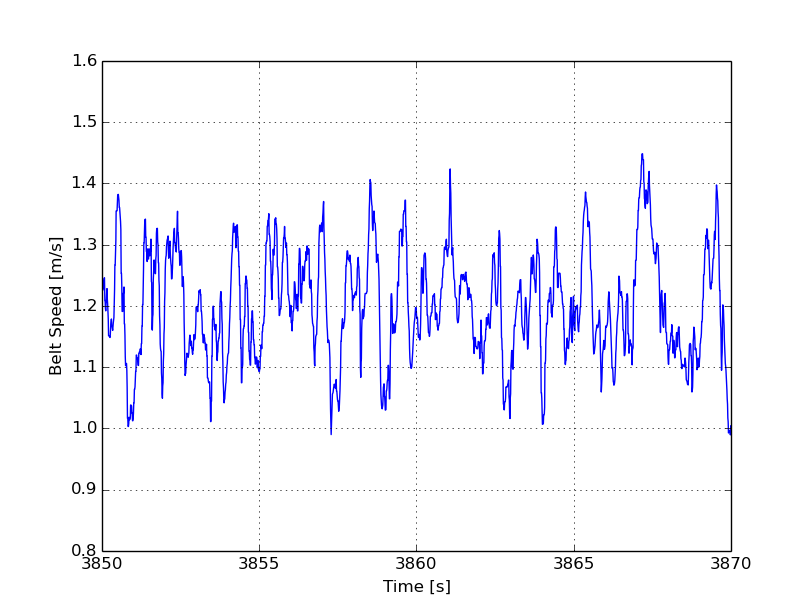
Random Belt Speed Variations

Measurement Variations

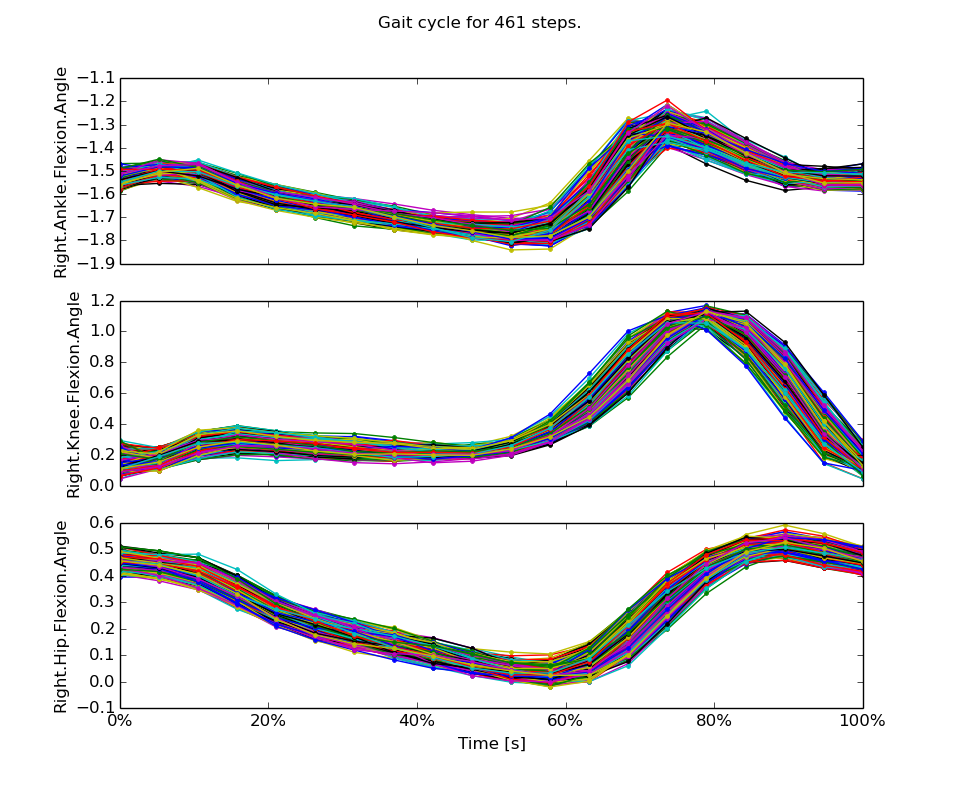
Measurement Variations

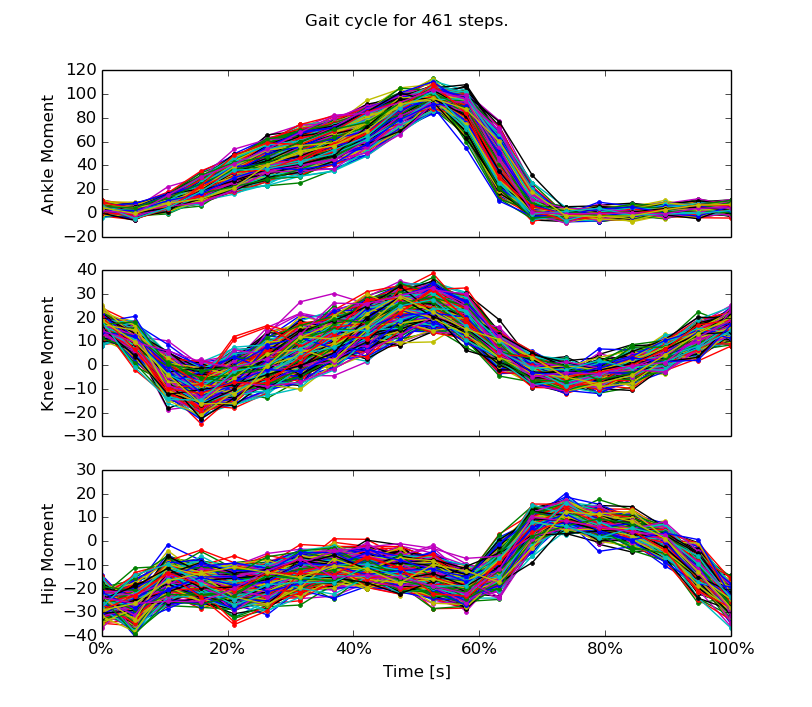
Gains: v=0.8 m/s

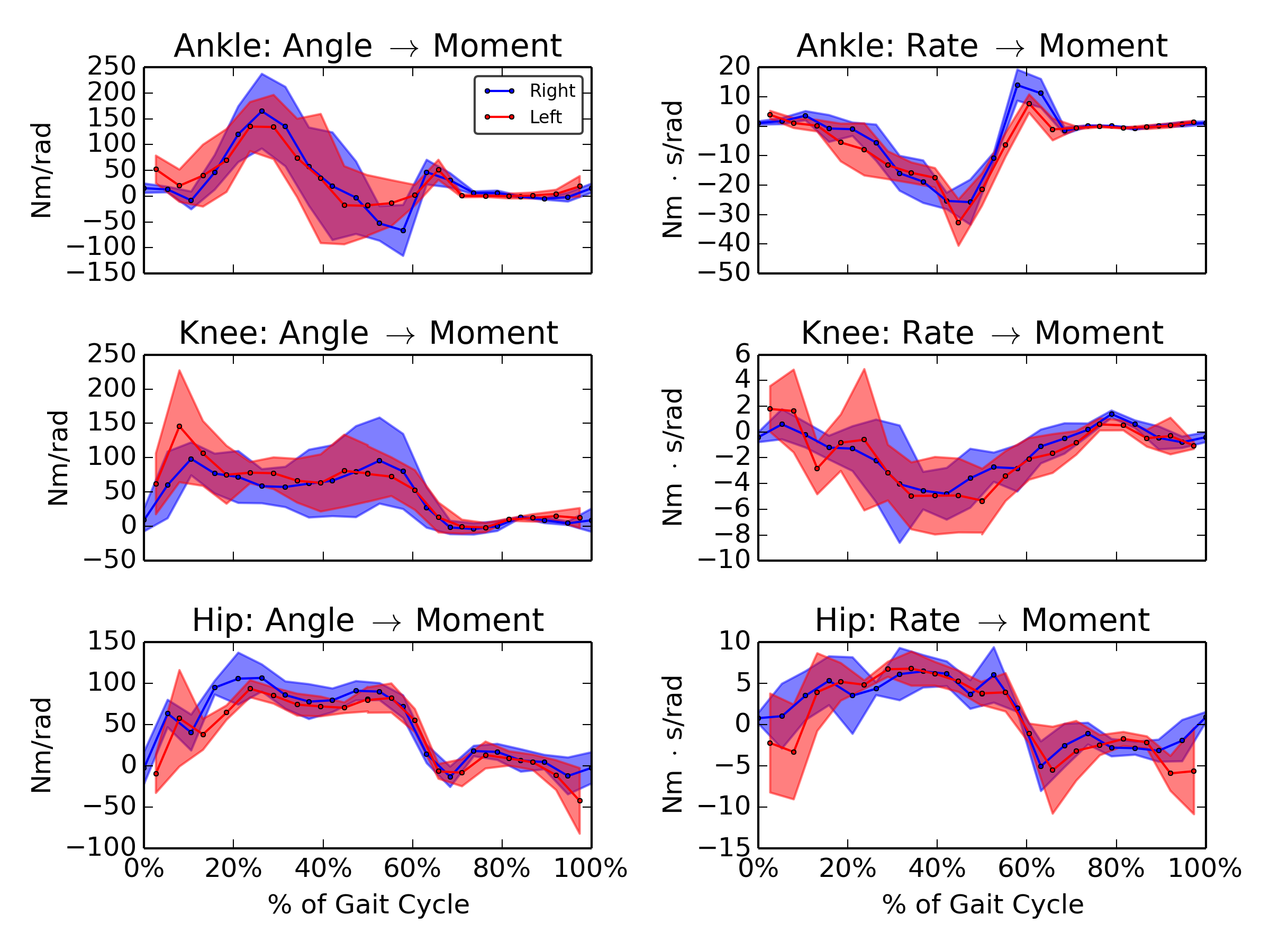
Gains: v=1.2 m/s

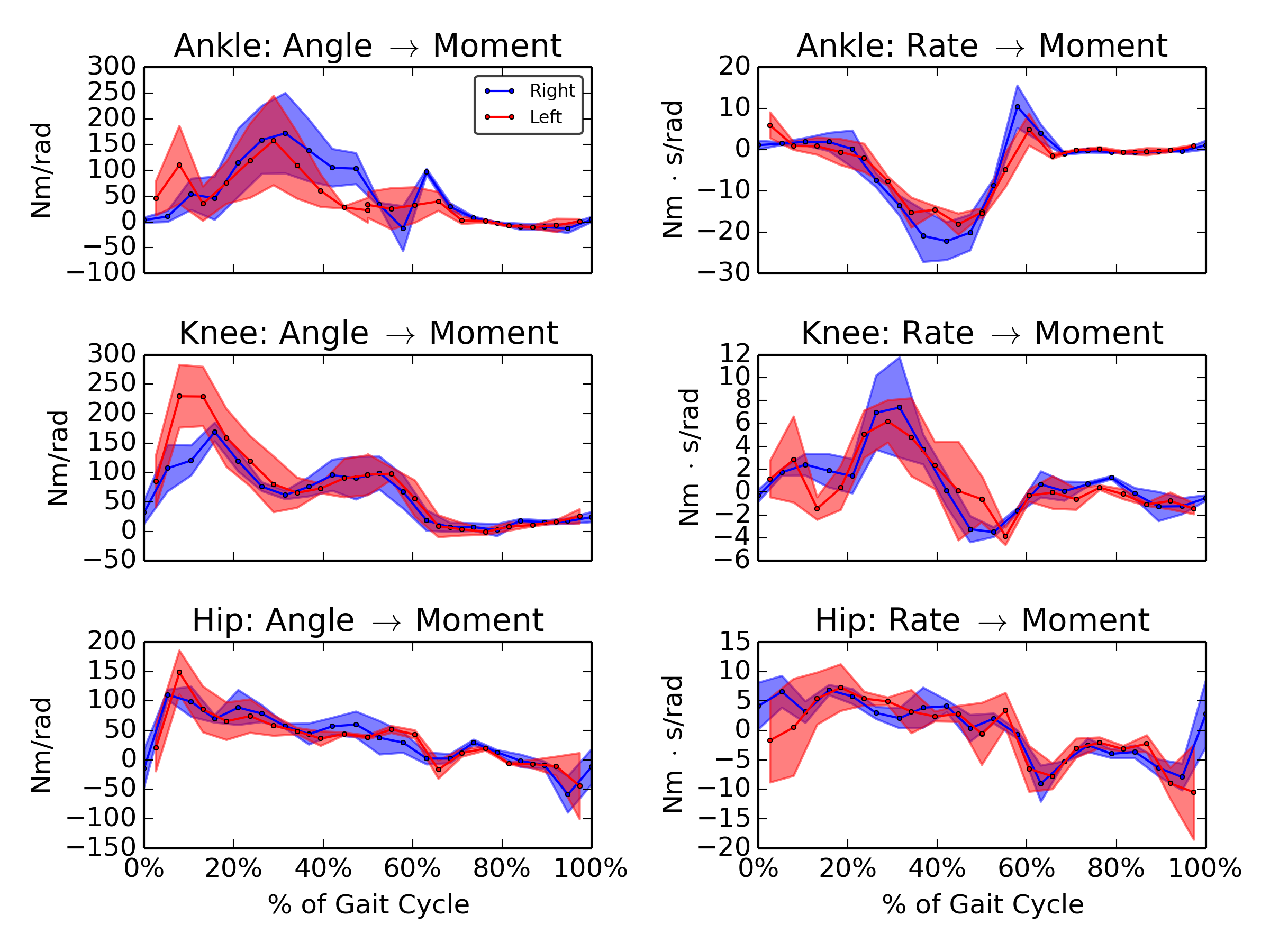
Gain variation with speed

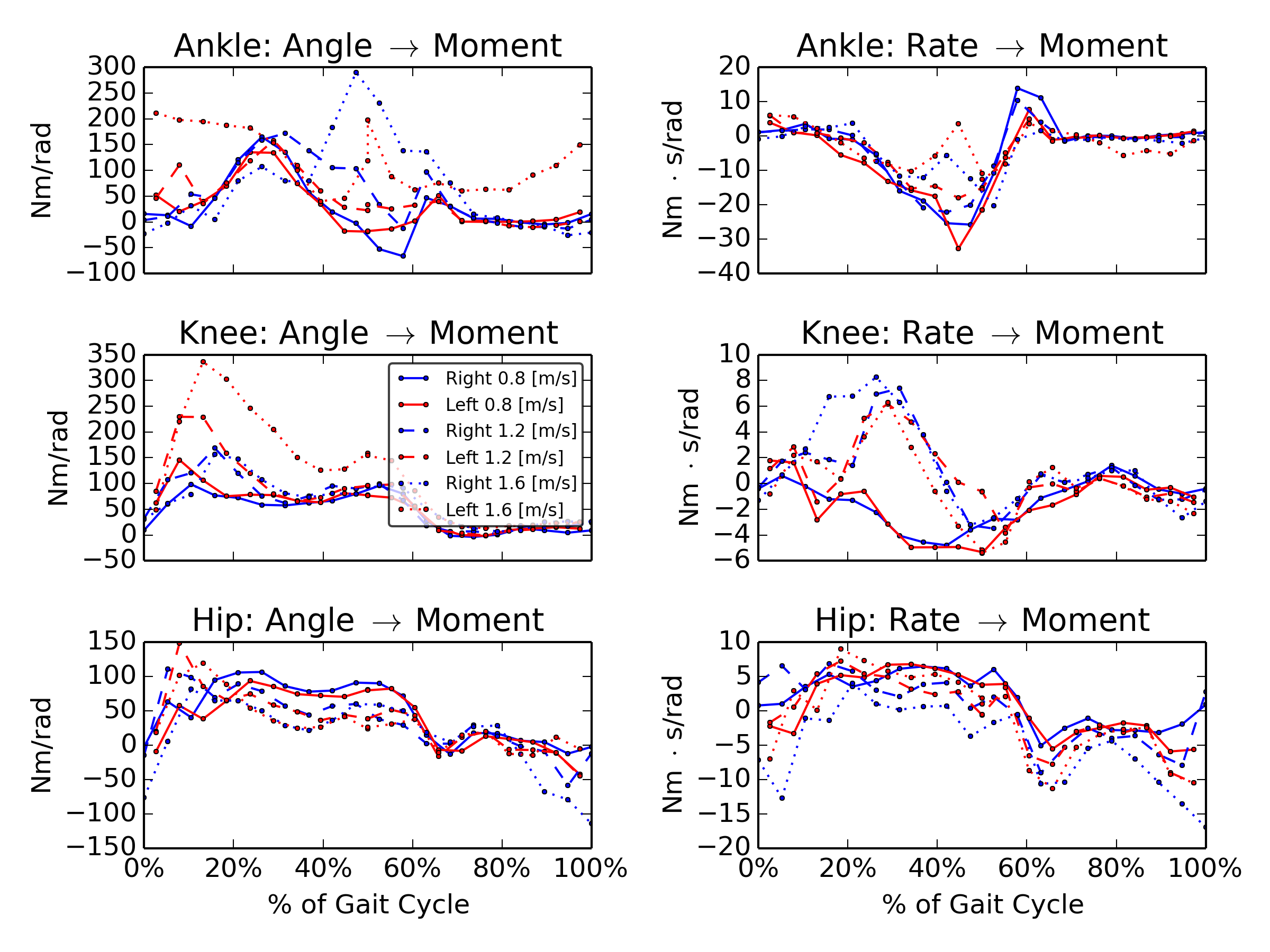
How good is the model?

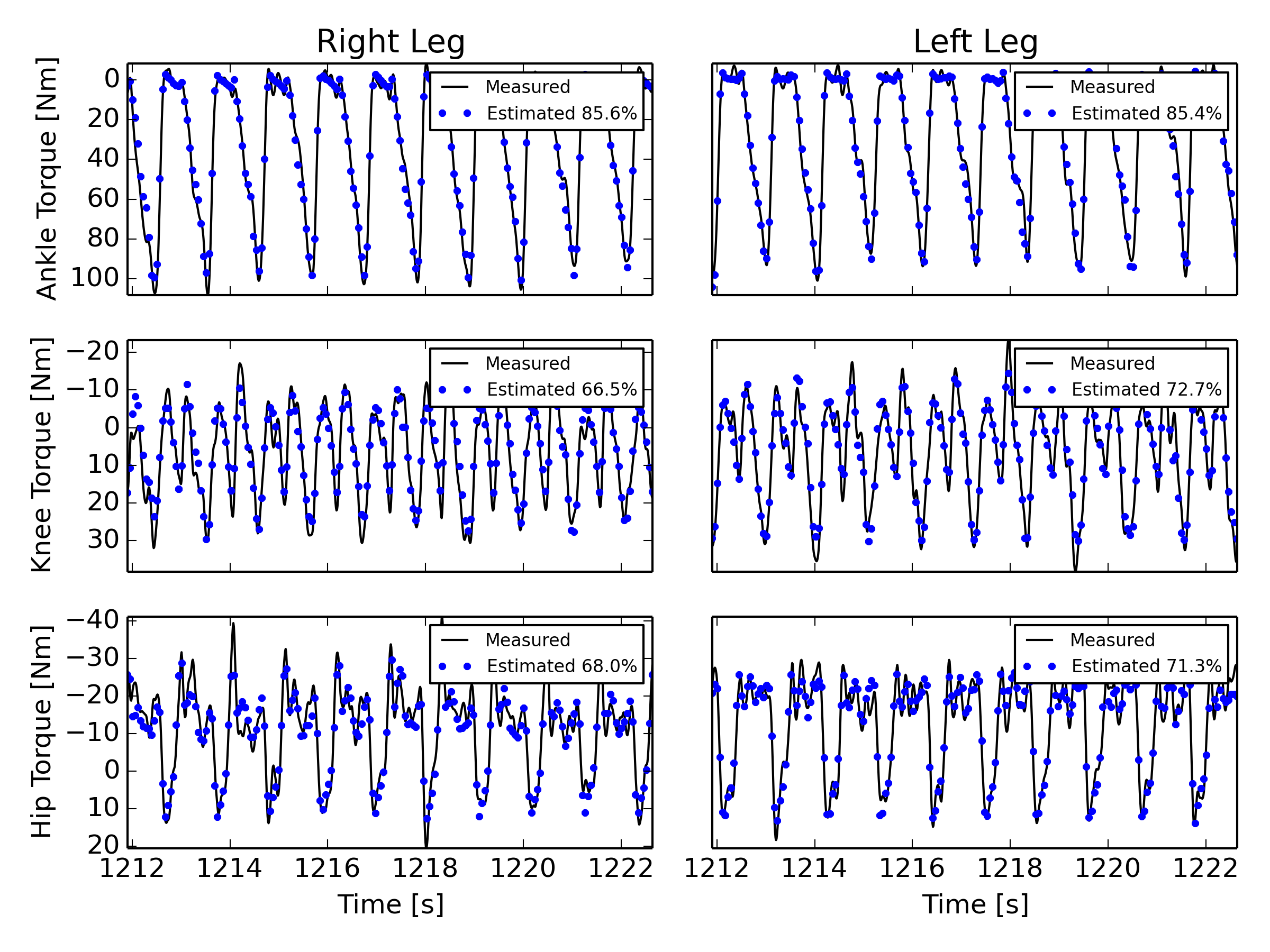
Summary

• Perturbations must be significantly higher that internal system noise to have any hope of estimating control in this fashion.
• Similar gain patterns in each leg.
• Similar gain patterns and magnitudes in different subjects.
• The model can predict the joint torques for independent data.

Future

• Explore full $\mathbf{K}$ matrix.
• Add in time delays.
• Remove clock from controller.
• Non-linear control models: e.g. neural network.
• Use indirect system identification approach with plant model.
• Try out the controller on a simulation that has open loop control.
• Try out the controller on the Indego exoskeleton.

Tutorial

Simulation and Control of Biomechanical Systems with Python

Tonight at 6pm

Chemistry Computer Lab in the Whitby building on the 2nd floor. Next to ASEC (previous location).

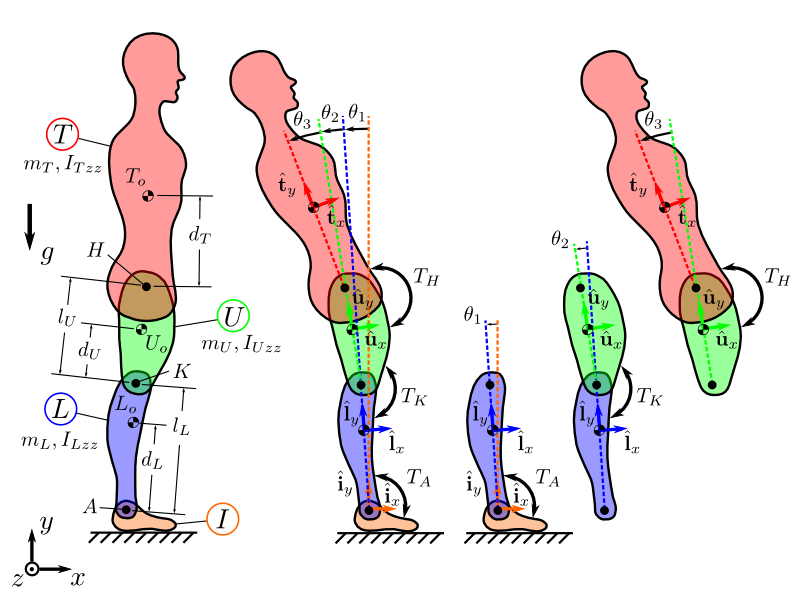
Information

Contact

• HMC Lab: hmc.csuohio.edu
• My website: moorepants.info
• Email: j.k.moore@csuohio.edu

Slides

• github.com/moorepants/MASB2014

Source code for this analysis

• github.com/moorepants/walking-sys-id
• github.com/csu-hmc/Gait-Analysis-Toolkit

Data

• On its way!