ENG 004 Lecture 8, Oct 23, 2012

Announcements

• Homework #3 due now
• Homework #4 will be posted after class
• Midterm coming up on Thursday, November 1
• Read Chapter 4

Topics

3D primitives and model types

Constructive Solid Geometric Modeling

3D Primitives

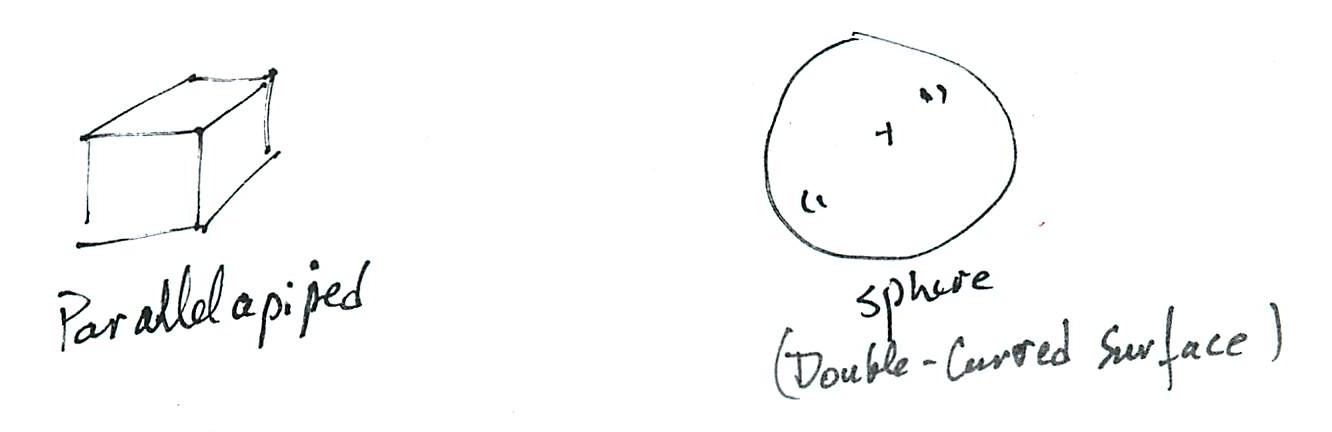
3D Primitives

3D Primitives

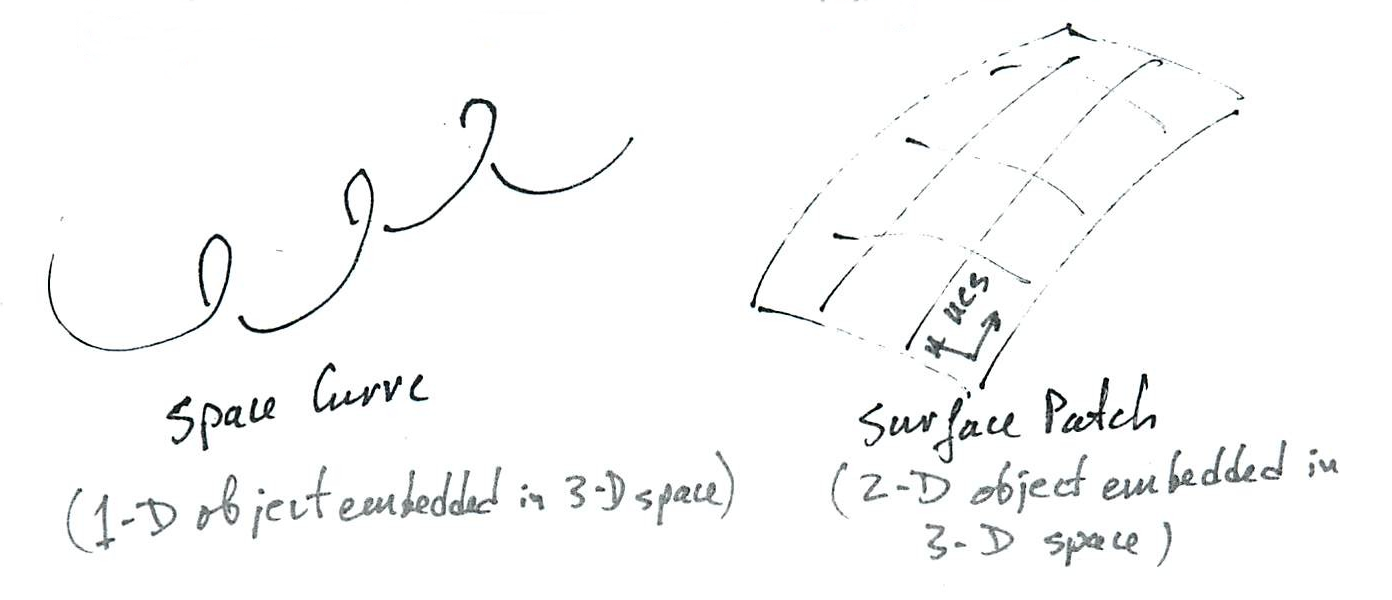
3D Primitives

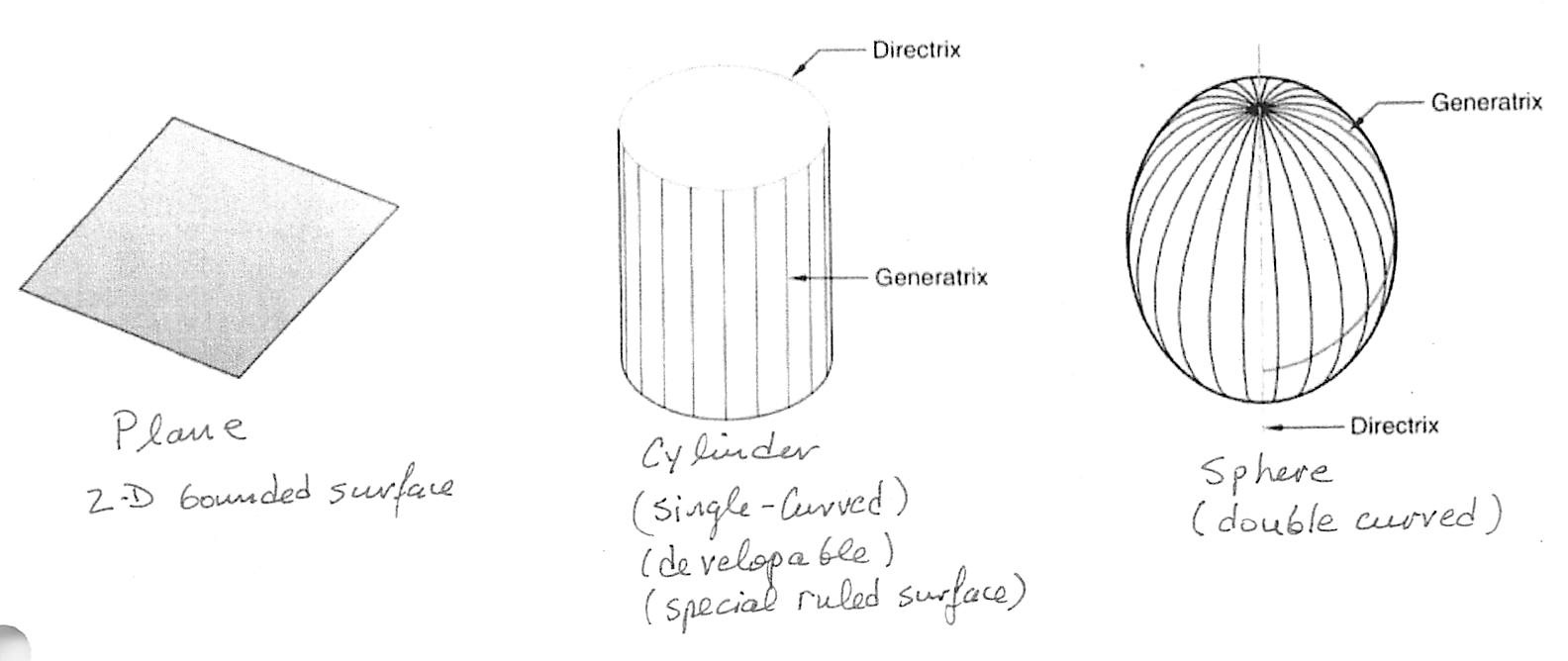
3D Primitives

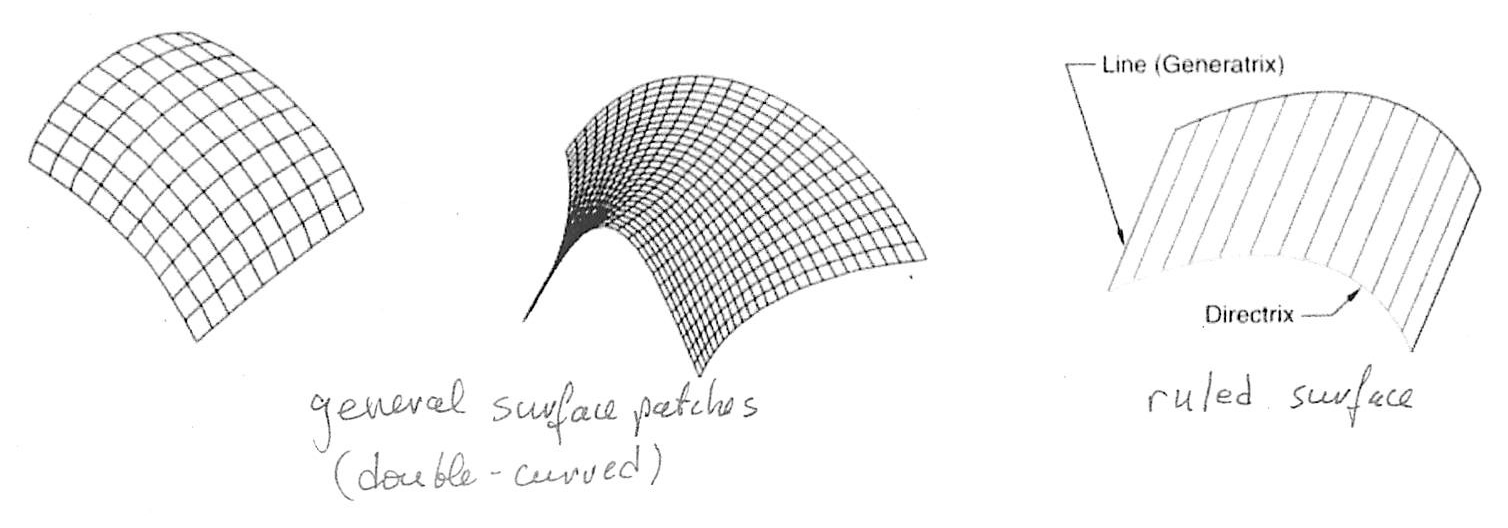
Ruled Surfaces

Undeveloped Surface

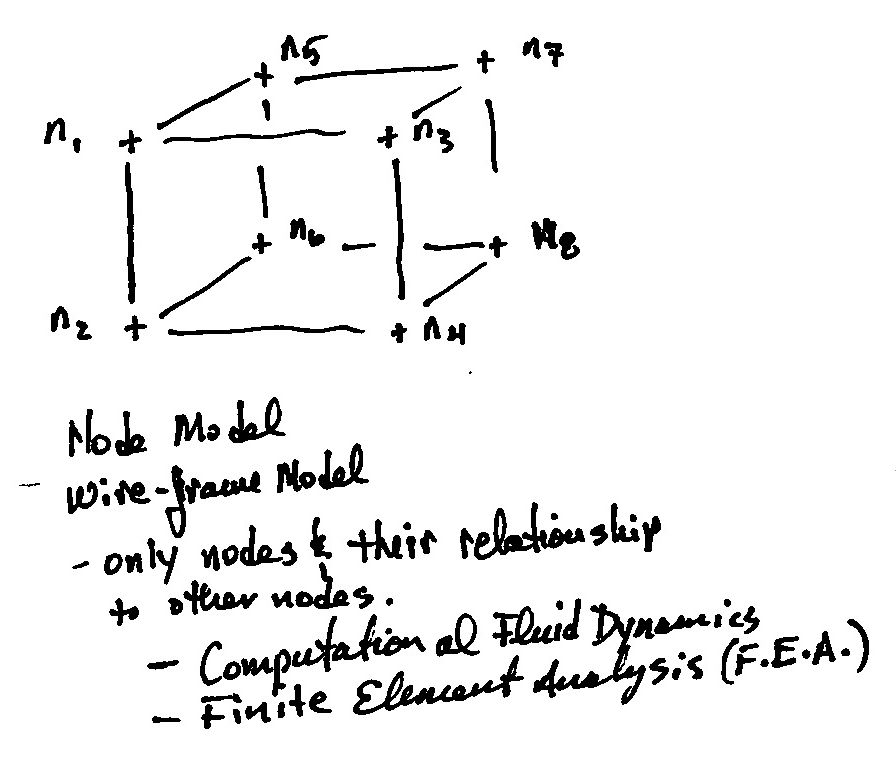
3D Modeling: Node Model

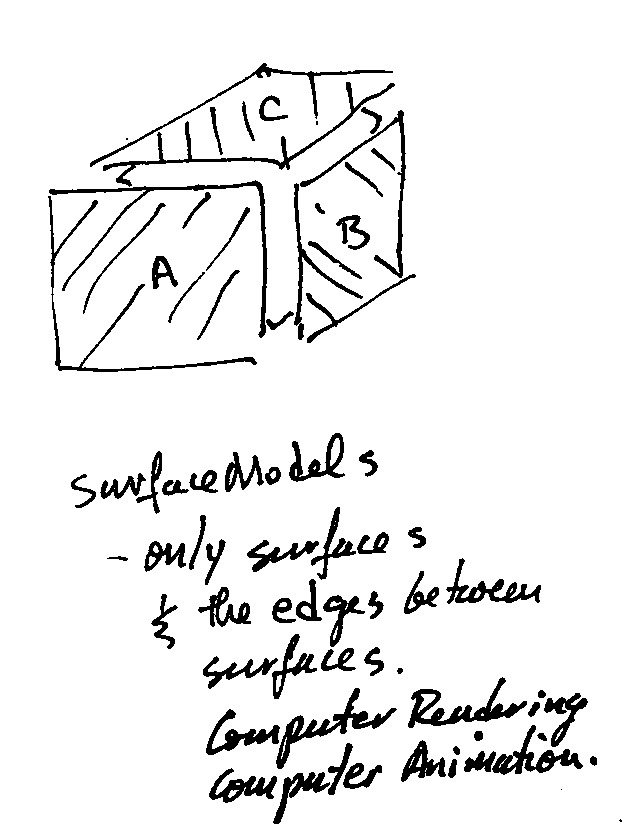
3D Modeling: Surface Model

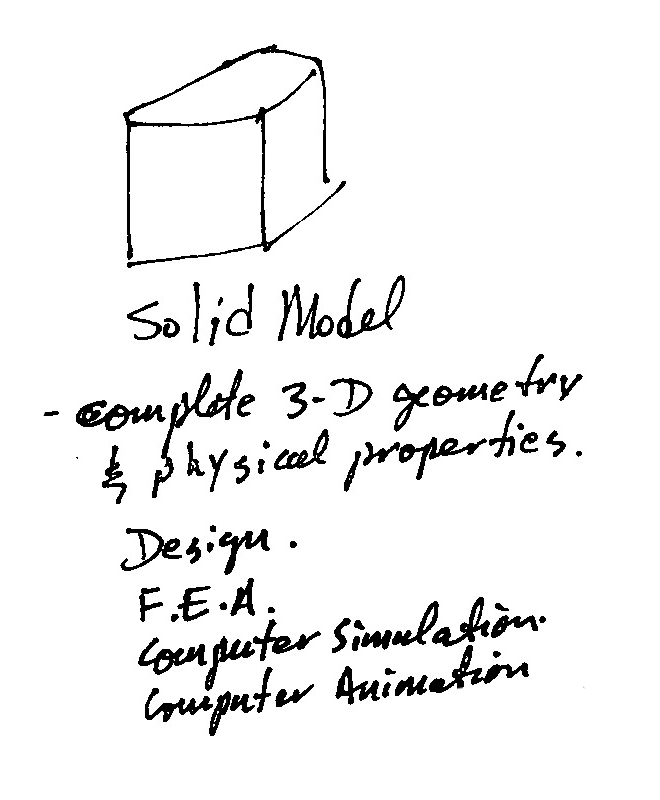
3D Modeling: Solid Model

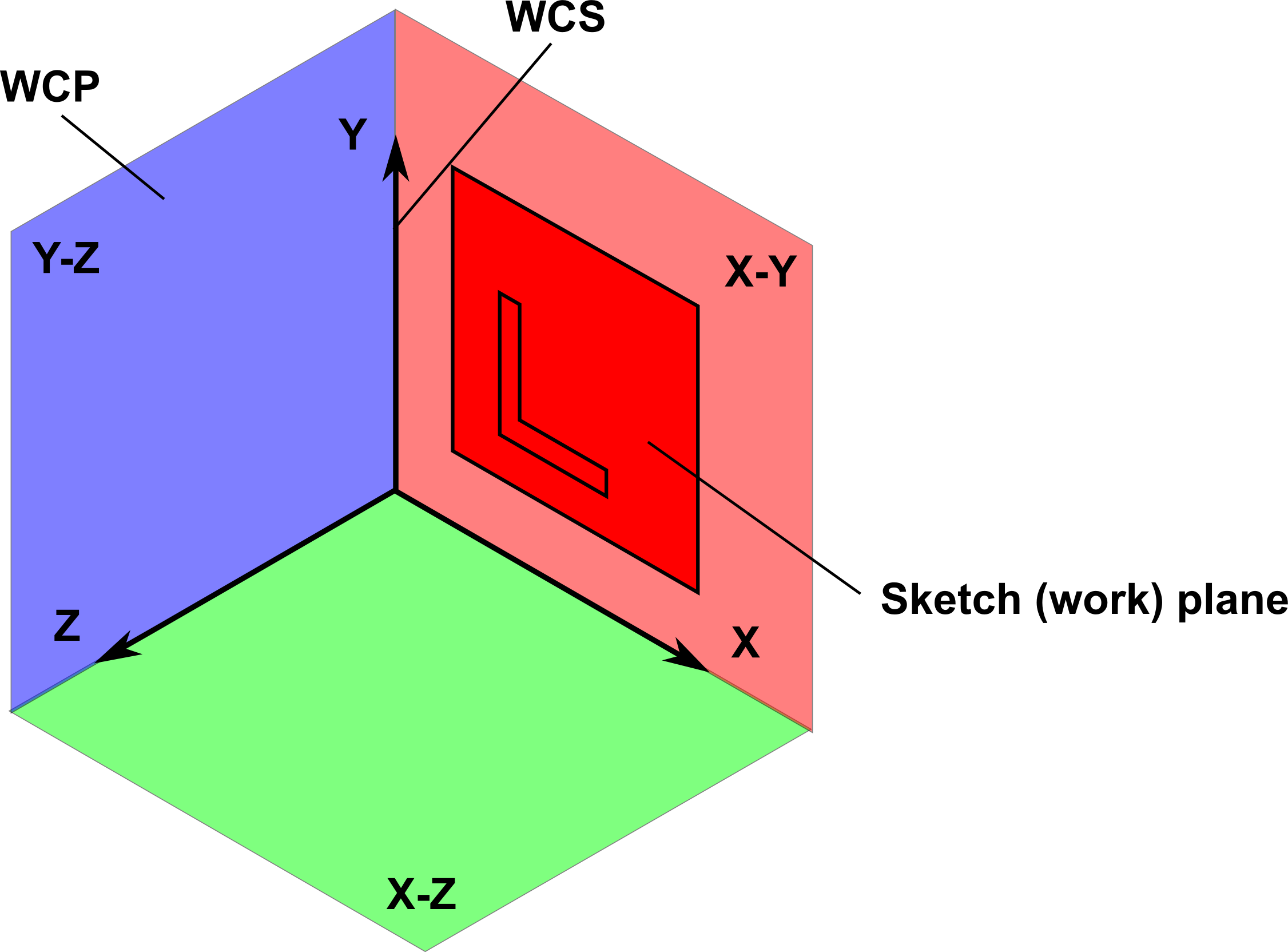
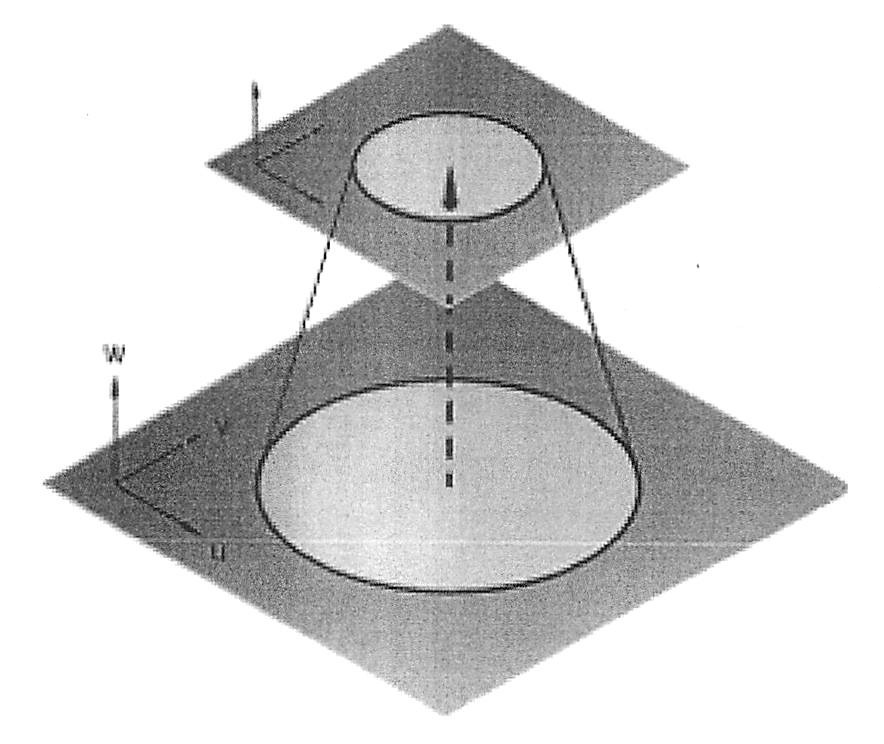
Sketch Planes

World coordinate planes (WCP) are associated with the world coordinate system (WCS) Sketch (Work) Plane Coincident or relative to a WCP Can be a plane or projected plane that already is in the model

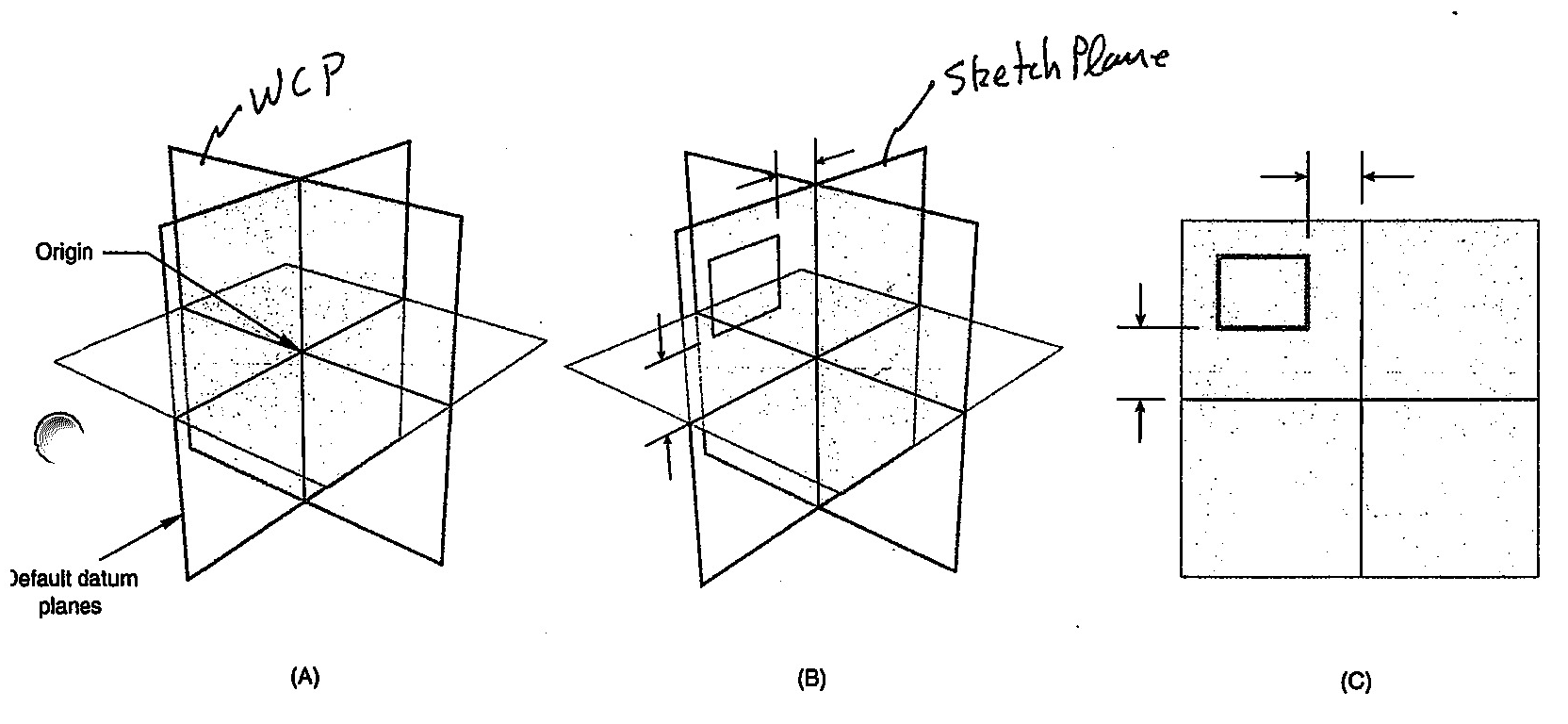
Sketch Plane Creation

Solid Model Boolean Operations

Constructive solid geometric modeling (CSG) uses Boolean operations and constructive operations to create a solid model.

Boolean operations

• Join (Union, Add): ∪
• Difference (Cut, Subtract): -
• Intersection: ∩

In order for Boolean operations to be logical, the features must be either overlapping or touching.

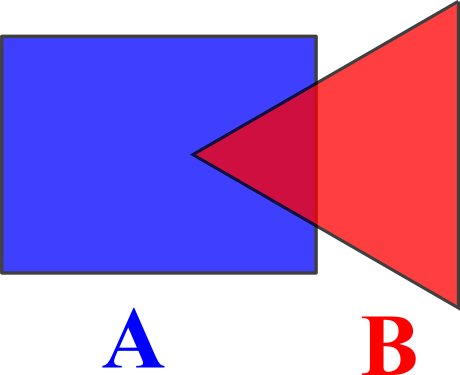
Boolean Operations: Union

Boolean Operations: Intersection

Boolean Operations: Difference

Boolean Operations: Difference

Solid Model Constructive Operations

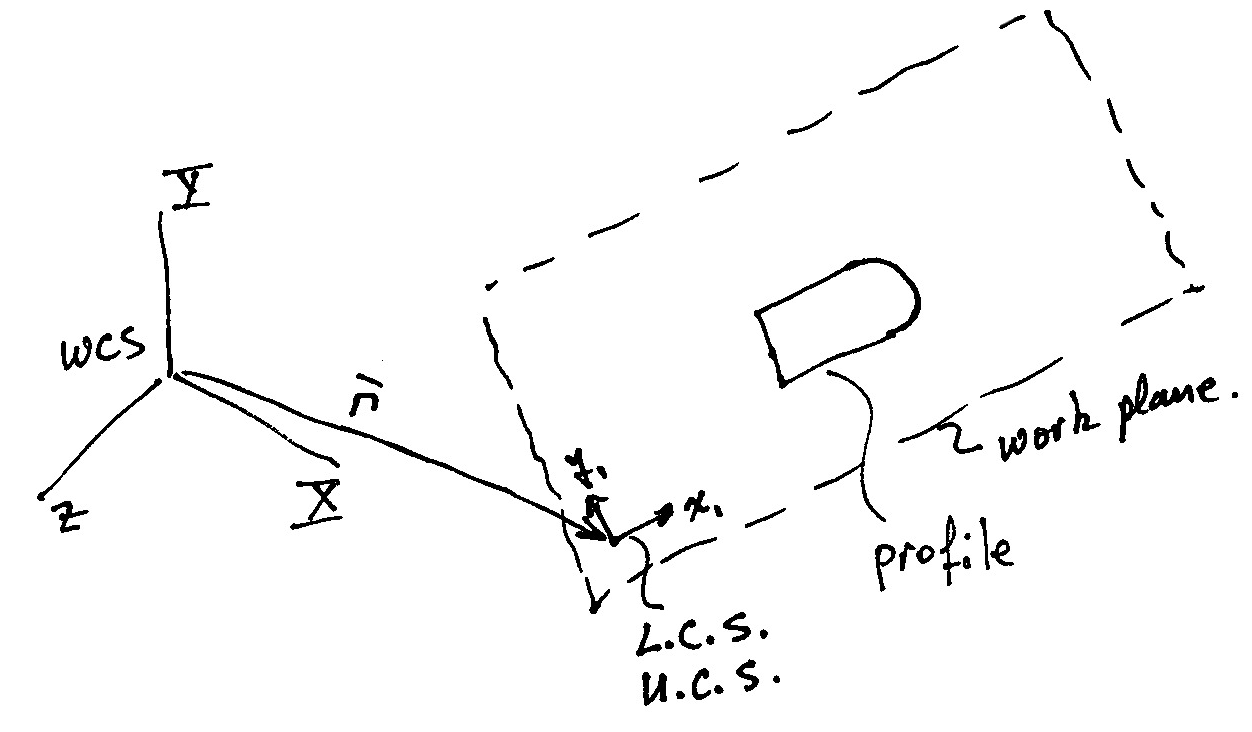
Define a work plane Define a closed profile (sketch) using 2D primitives Infinite, unbounded 2D plane placed and oriented anywhere in the 3D domain of the model A local coordinate system (LCS) or user coordinate system (UCS) is associated with the World Coordinate System (WCS) A 2D profile is defined

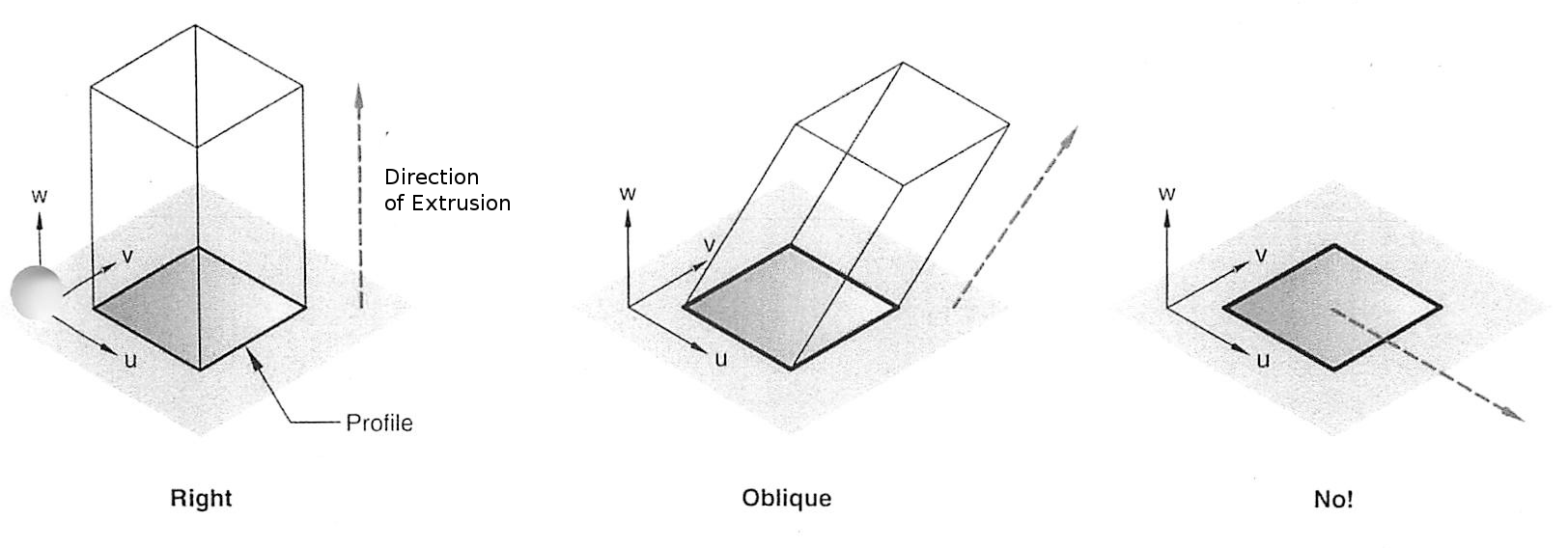
Extrusion

Revolution

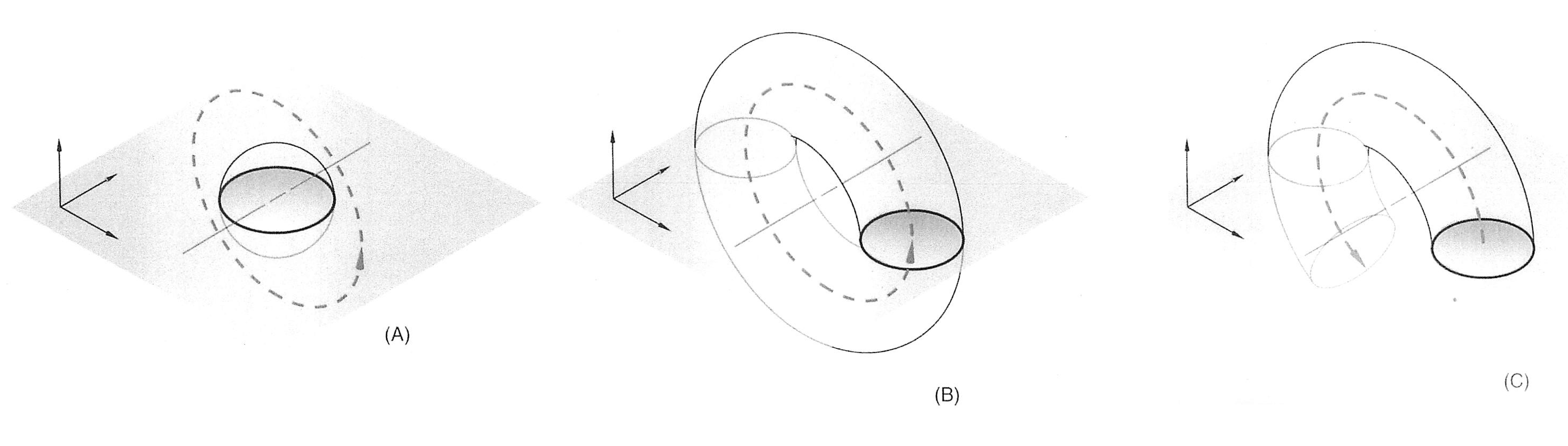
Revolution

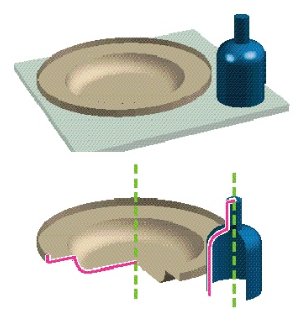
Sweep

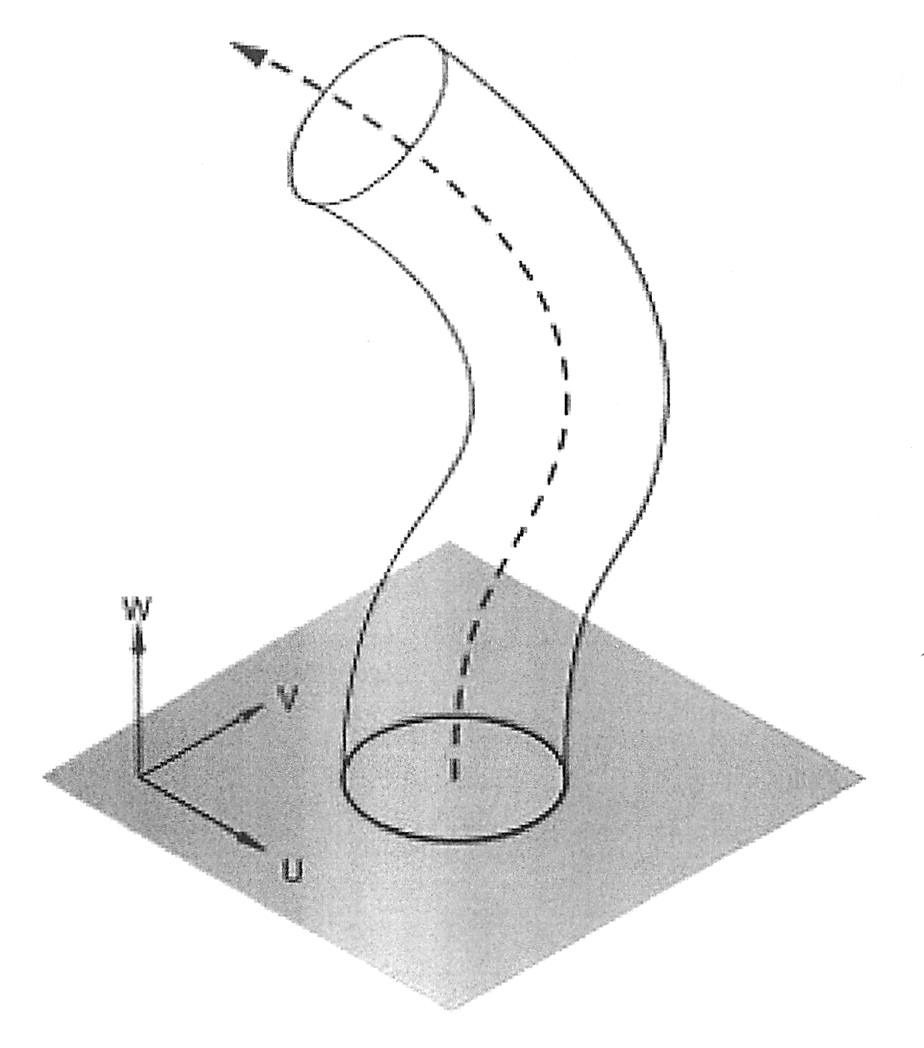
Loft

Constructive Operations

Extrude (linear sweep)

Define length and direction of the extrusion. The direction cannot be parallel to the work plane.

Revolve

Define the axis and amount of rotation

Sweep (path based sweep)

Define a space curve along which the sweep occurs

Loft

Define a space curve and intermediate profiles along the curve.

Feature Planning

• History tree
• Logical sequence of procedures used to create a solid model
• There is no unique history tree for a particular part being modeled

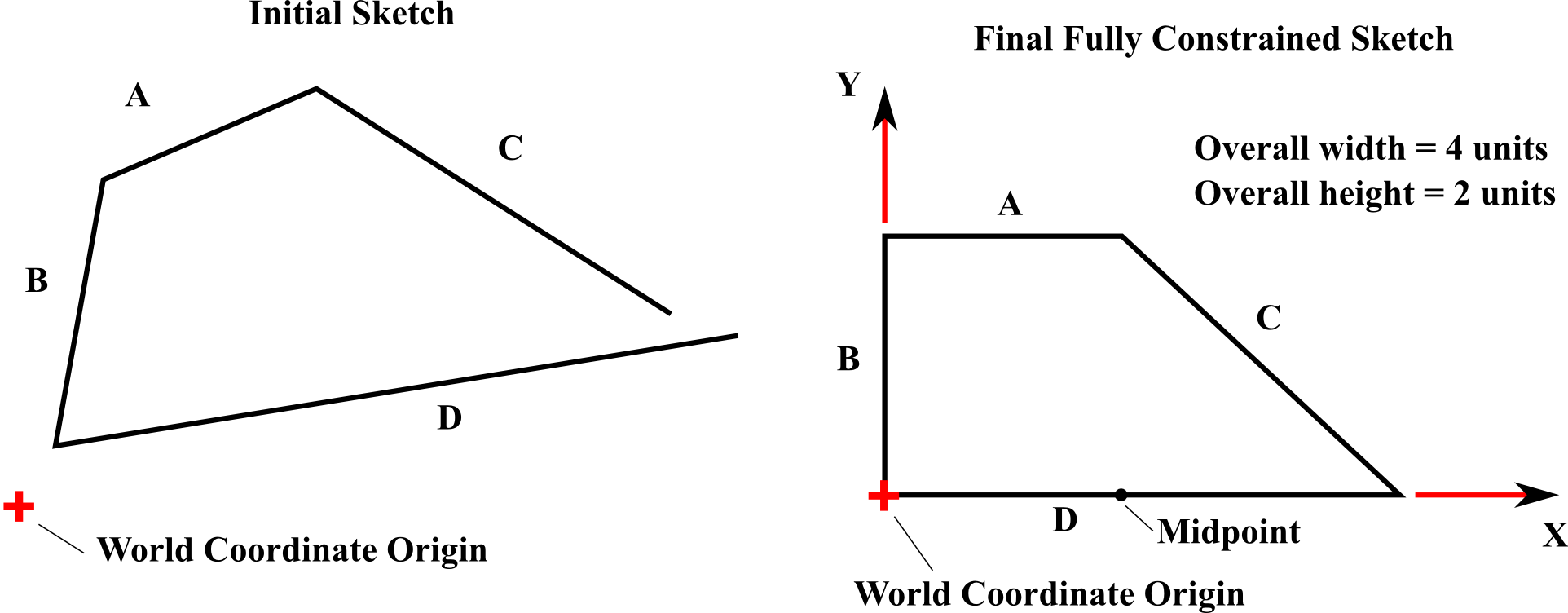
Sketch Constraint Quiz

pg 117 for constraint types, groups of 3-5, all names on one paper