How WE RIDE Bicycles
Introduction
Human control of bicycle dynamics with experimental validation and
implications for bicycle design
Researchers
Dale L. Peterson
Jason K. Moore
Ron Hess
Mont Hubbard
Sports Biomechanics Laboratory
Mechanical and Aerospace Engineering Department
University of California, Davis
Ability vs. Understanding
(Almost) everybody knows how to ride a bike, but (almost) no one knows
how we ride a bike
Project goals
- Understand what we do while riding a bike.
- It doesn't study "How people learn to ride a
bike"
- but rather "What they are doing after they know how"
Motivation: Theoretical and Practical
- Bicycles are an economical platform for understanding human control of
dynamic systems.
- Roughly half our energy use and carbon footprint is for
transportation.
- More than 50% of our trips are less than 2 miles, ideal for
bicycles.
- Bicycling and walking will eventually become a larger share of our transportation solution; sooner is better.
- Knowing how we ride, and how bike design affects this, can help in bicycle design for outlier populations like elderly and children and promote more biking.
How can we do this?
What is a dynamic system?
A system that changes in time. It has:
- State variables
- Inputs
- and often Control
Example dynamic system with feedback control
- Balancing stick or broom balancer
- Differential equations describe how the stick falls
- Human senses position (and much more) and executes corrective action to
move hand
Bicycle Human Feedback
On the bicycle, human sensory organs include:
- visual system
- inner ear otolith organs (vestibular)
- tactile sensors in skin (proprioceptive)
and sense quantities like
- rotation rates
- limb position
- speed and direction
- error in position
- etc.
Bicycle Human Feedback
Brain integrates all this information in real time to produce a single
control signal that actuates muscles to turn handlebar. This is the process
we study.
Our project is famous and award winning!
Washington Examiner
Our project is famous and award winning!
Senator Tom Coburn R-OK

Taxpayers may also question the value of many of the projects NSF actually
chose to fund, such as: How to ride a bike...
Organization
- Luke Peterson
Bicycle dynamics without rider
- Ron Hess
Theory of human control
- Jason Moore
Experimental identification of rider control
Bicycle Dynamics 101
What/Why/How are we modelling?
- What: Motion – Dynamics
- Why: Understand the influence of physical parameters on “stability” and “handling”.
- How: Apply Newton’s Laws to obtain differential equations which
describe how the bike moves.
Modelling Assumptions
Start simple!
- Rigid parts (two wheels, frame and fork)!
- Rider rigidly attached to the frame!
- Frictionless joints!
- No slip rolling!
- No aerodynamic affects!
Even with these simplifications, we still have 25 parameters to keep track of.
What do we observe in real bicycles?
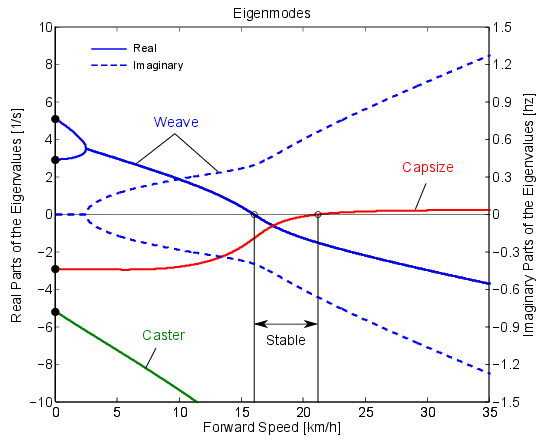
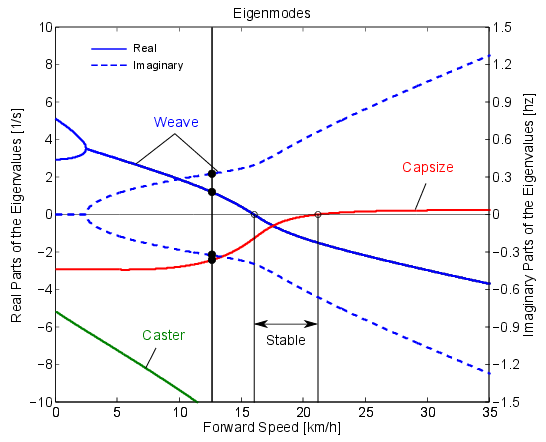
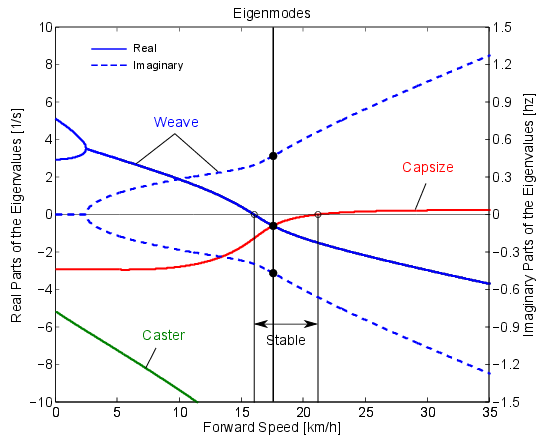
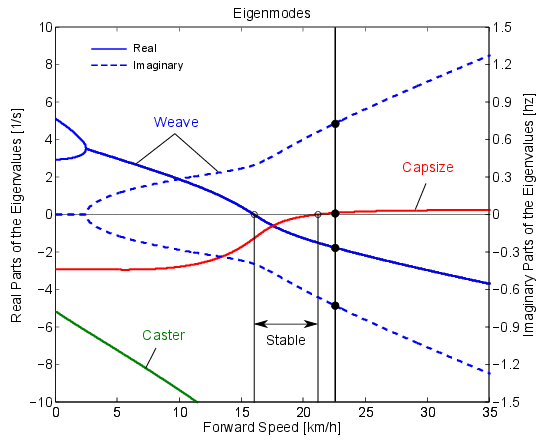
Is the motion stable?
Unstable at 0 km/h (0 mph)
Unstable 12.6 km/h (7.9 mph)
Stable at 17.6 km/h (11.0 mph)
Unstable at 22.7 km/h (14.2 mph)
Stability of upright motions
Counter-steer
Unconventional bicycle with stability
What is observed? Unconventional bicycle with stability
Turning Bicycles
Stability of turning motions employs same mathematical framework
Key Differences
- Straight line riding is an equilibrium at any speed, perhaps
stable in a range of speeds. No rider steering input need for stable
speeds.
- Turning bicycle: for constant v, turns of different R
will require different lean, steer, and steer torque. Rider must apply constant steer torque.
- More difficult to test experimentally.
- Stability of turning motions is an active area of research.
Robotic Bicycle
Why?
- Eliminate confounding factors of human rider.
- Quantitative comparisons of model and experiment.
- Test different feedback control techniques.
Robotic Bicycle Experimental Setup

Robotic Bicycle
- System identification of upright motions and turning motions:
- Apply precise inputs (motor torques)
- Measure response (angles/rates/accelerations)
- Test the validity of modelling assumptions:
- Under what conditions is the pure rolling assumption reasonable?
- Is rigid-body assumption reasonable?
- Are frictionless joints appropriate?
- Improve the model as needed.
Challenges
- Real time data acquisition, control, logging, remote monitoring.
- Detecting "crash" conditions and responding safely.
Theory of Human Control
Bicycle + Rider = Balance?

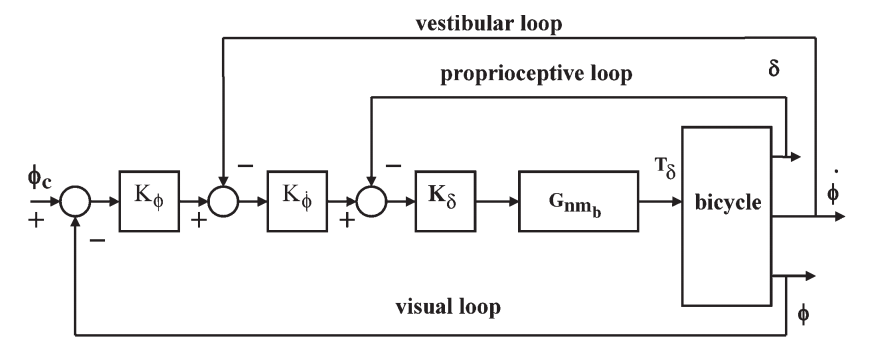
Feedback Model
Basic model will include:
- Visual, proprioceptive and vestibular sensory feedback
- Rudimentary neuromuscular model
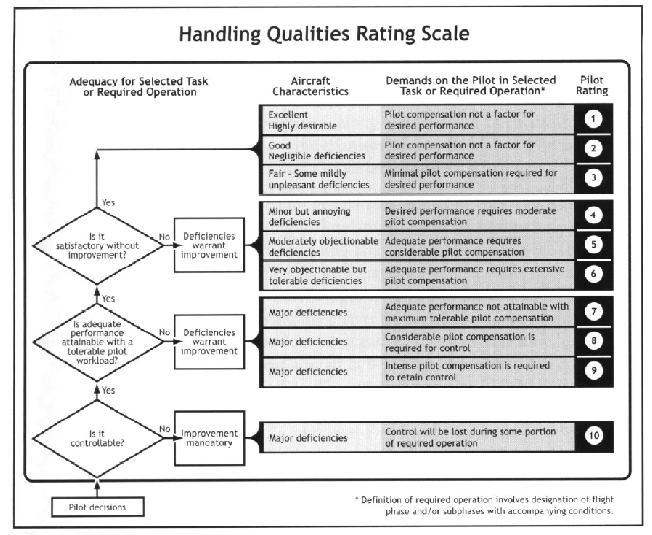
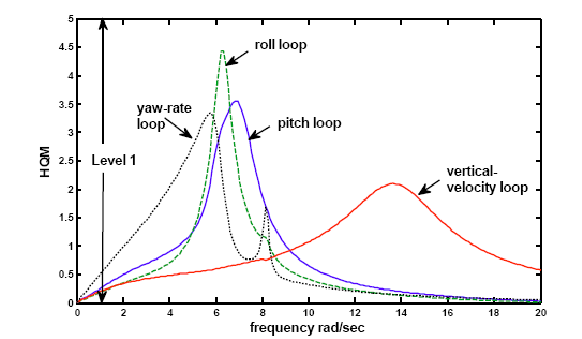
How pilots rate aircraft “handling qualities”
Handling qualities and the helicopter pilot
Predicting a bicycle's handling qualities
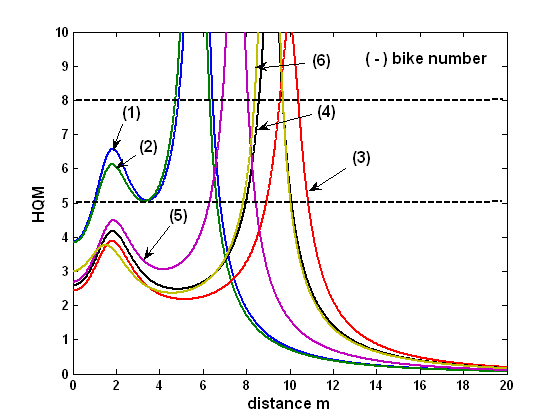
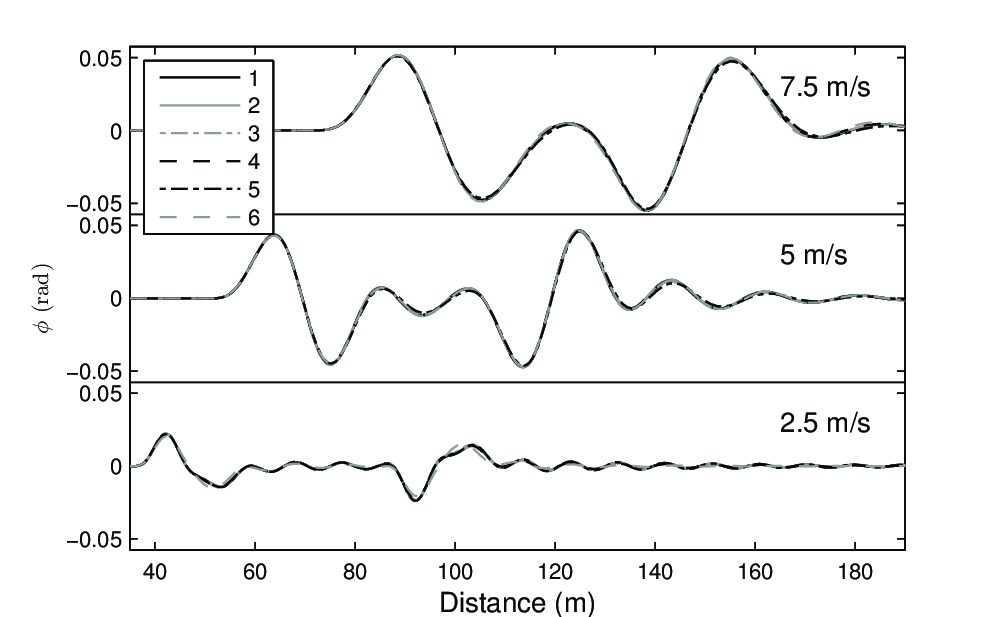
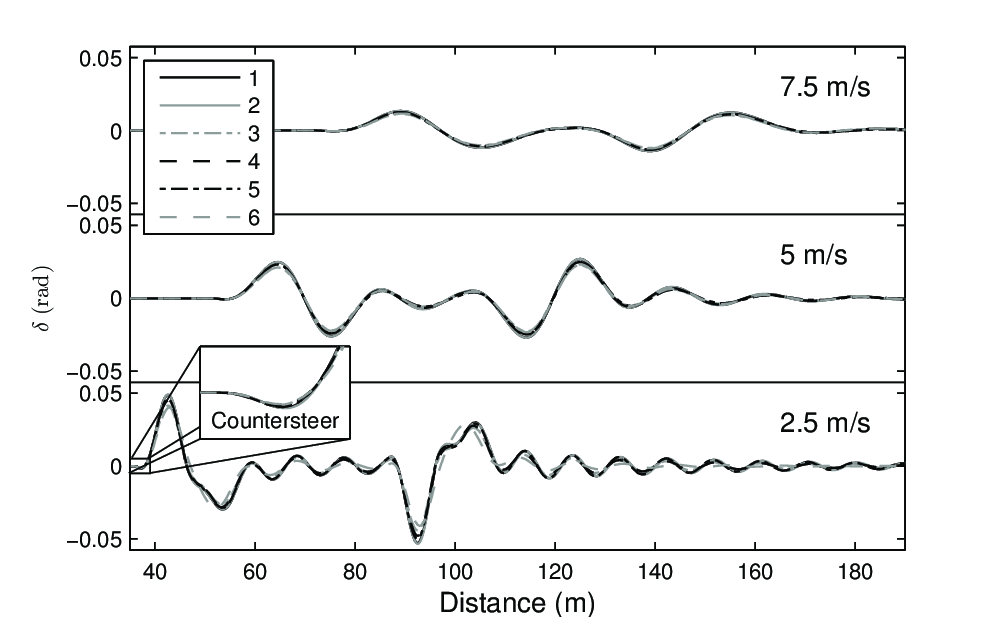
V = 2.5m/s
|
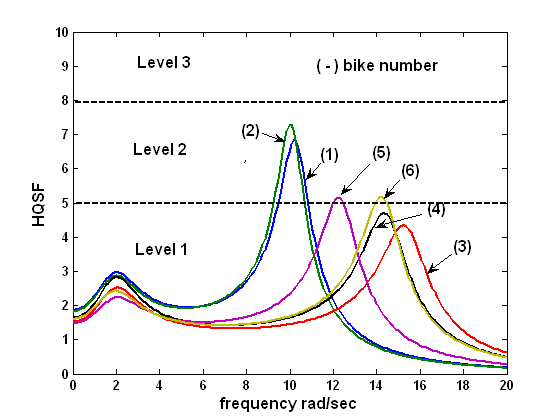
V = 5m/s
|
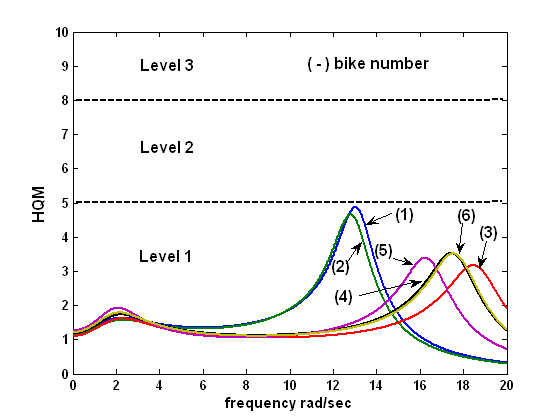
V = 7.5m/s
|
Bicycle Control at Slow Speeds
Professor on a bicycle
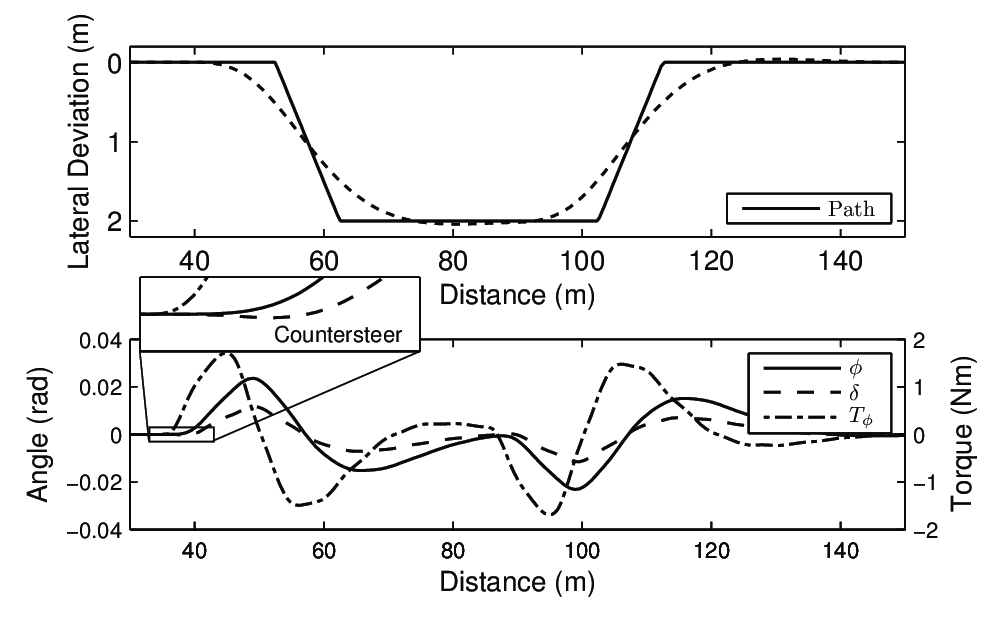
Rider Model Results in Lane Change Maneuver
Roll angle with rider control.
Rider Model Results in Lane Change Maneuver
Steer angle with rider control.
Rider Model Results in Lane Change Maneuver with Hands Free
Rider model + bicycle in lane change with
hands-free
Identifying the Rider + Bicycle System in Experiments

Instrumented bicycle
|
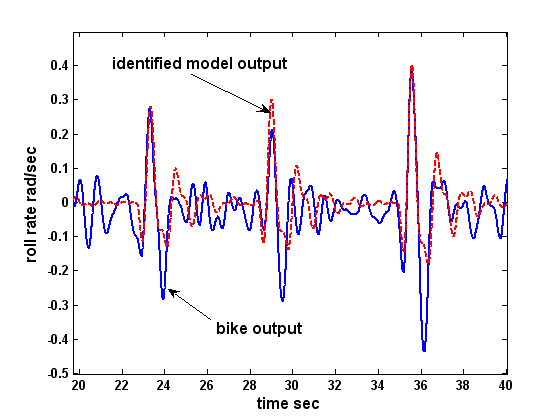
Identification results rider + bicycle
roll-rate response to pulsive side forces
|
Experimental Identification of Rider Control
Start Experimenting: On the treadmill
Professor can now balance!
Start Experimenting: Outside
Notice the counter-steering.
Balance with your body
Back to the Treadmill

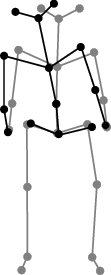
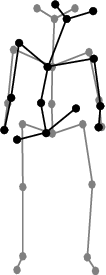
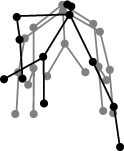
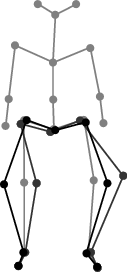
Kinematic Motion Data
Motions and Groups
Steer-Roll-Yaw
Motions and Groups
Pedaling
Motions and Groups
Lateral Knee, Knee Bounce
Instrumented Bicycle

Lane Change
Random Disturbances
How do we ride bicycles?
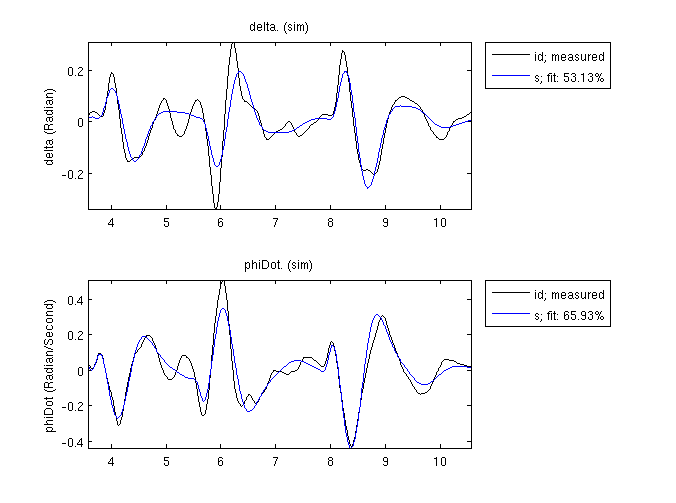
Bicycle control is adequately modeled by a linear state feedback control
system which is parameterized by five gains and a neuromuscular frequency.
Wrap up
- Better understanding of human control
- Better understanding of human/machine interaction
- Tools to analyze bicycle designs
- New bicycle designed to handle well for particular situations
Possible new bicycle designs
This work was supported by Grant NSF CMMI-0928339 from the National
Science Foundation.
←
→
/
#